Understanding Tendon Primary and Tendon Secondary

Understanding Tendon Primary and Tendon Secondary

Table of Contents

1. Introduction

2. Hyperstatic (Secondary) Actions

3. Prestress Loads in midas Civil

4. Example Problem

5. Conclusions

6. References

Please fill out the Download Section (Click here) below the Comment Section to download the Ebook!

1. Introduction

Prestressed beams are made continuous over the supports to increase the structural integrity. A continuous beam provides an alternate mechanism for load distribution in the event of failure of the section. In the region of high seismic zones, continuous beams are preferred as it provides redundancy in the load path, i.e., the possibility of formation of hinges in case of extreme events. Continuous beams are statically indeterminate structures. For continuous prestressed bridges, vertical load capacity is more and lesser mid-span deflection for the same span and section. The depth of the section to be adopted in continuous sections can be less than a simply supported beam for the same span. This can be reduced the number of deck joints and bearings and proved to be economical in material use.

The stresses at the top and bottom fibers are calculated to compare with the allowable stresses to analyze the prestressed beam members at transfer and service loads based on the stress concept.

For a simply supported beam under uniformly distributed loads (UDL) and applied prestressed with constant eccentricity (e) along the span of the internal forces in the concrete.

 

 

Fig 1: Simply Supported beam under UDL

 

 

 

 

Fig 2:Stress profiles at a section due to internal forces

 

 

 

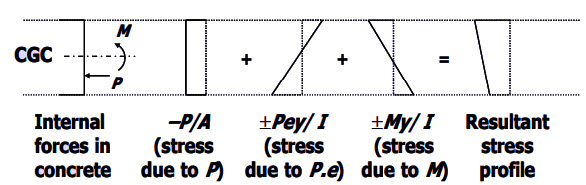
The resultant stress at a distance y from the Centroid of gravity of Concrete (C.G.C) by the superposition principle is denoted by the following expression. 

 

 

 

Equation 2: Resultant Stress by the principle of superposition

 

 

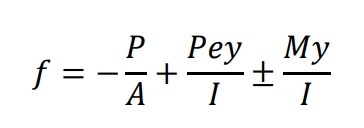
2. Secondary Actions (Hyperstatic) Definition

Secondary actions in prestressed members are developed due to prestressing forces which are the due degree of indeterminacy and constraints by the supports to the free movement of the prestressed concrete members. If members are allowed to displace freely, as in the case of determinate structures or pre-cast members before installation, no secondary moments will be generated in the structures. However, in the case of cast-in-situ construction, secondary actions can be significant and must be considered for design as supports restraint the movement of the prestressed members.

• When the Prestressing tendons apply load to the structure, the resultant forces and moments generated can be considered as a combination of primary and secondary or parasitic effects. No secondary moments are set up for a theoretical beam with a concordant tendon arrangement, but this rarely occurs in practice. The stage-by-stage construction sequence and envelope of loads applied to the structure inevitably result in a non-concordant prestress layout, and secondary moments can be significant.
• The secondary moments can often be beneficial by reducing the hogging moments at the piers but at the expense of increasing the sagging moments in the span.
• The primary effect of the prestressing is the moment, shear, and axial force generated by the direct application of the force in the tendon on the section being considered. Secondary effects occur when the structure is statically indeterminate, and restraints on the structure prevent the prestressed member from freely deflecting when the prestress is applied.

midas Civil converts pre-stress tendon loads applied to a structure into equivalent loads as described below

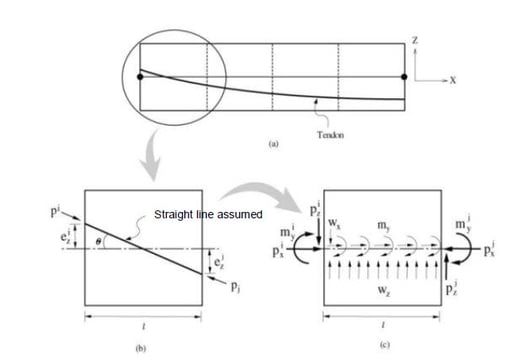
1. The tendon profile in each segment is assumed to be linear. The concentrated loads are calculated using equations (2) and (3), and equations (4) and (5) are used to calculate internal distributed loads. The internal loads are converted as equivalent loads applied to the elements. The time-dependent effects due to creep, shrinkage, and relaxation due to each of the construction stages.

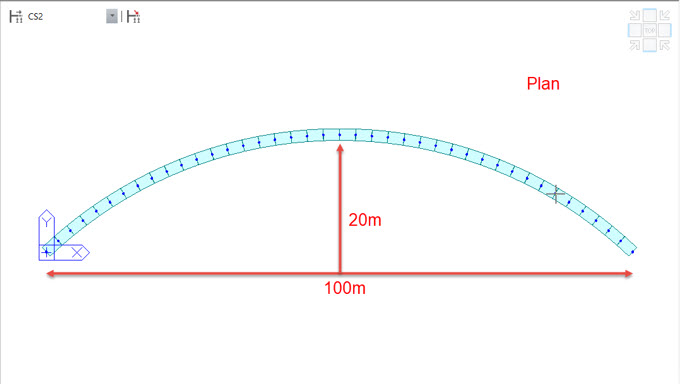
Problem Statement

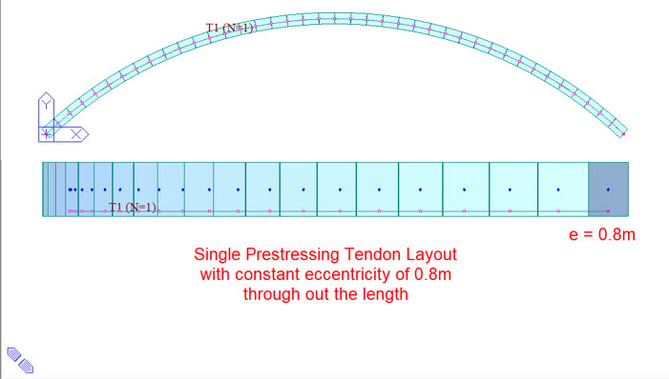
Calculation of Primary and Secondary Effects due to applied prestress of single tendon jacked from both the ends for the simply supported curved bridge.

 

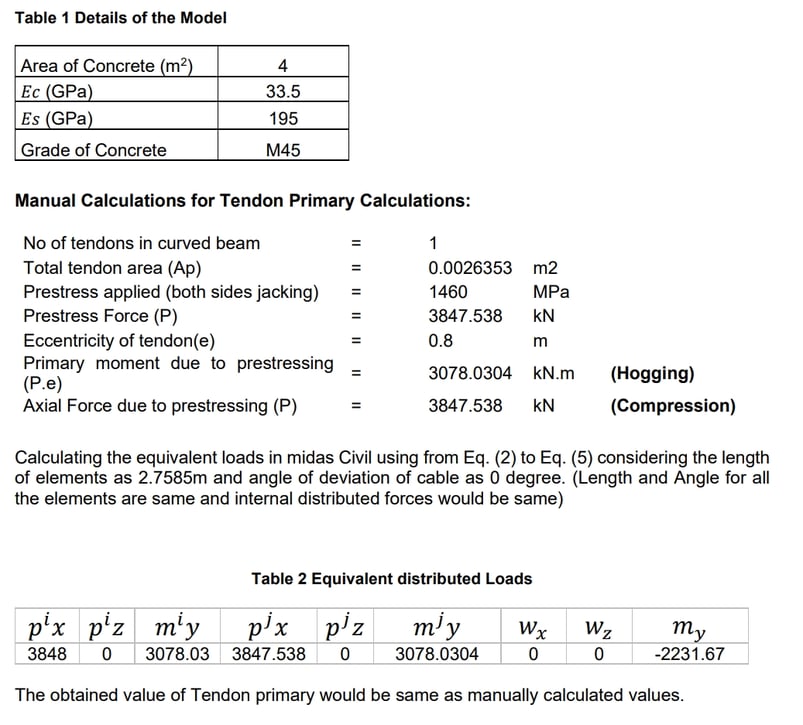
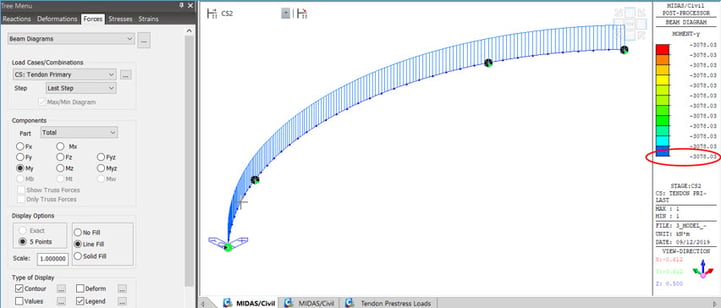
These above equivalent loads need to be applied to the model, and then we obtain the reactions

due to prestress effect or direct px, py, my loads can be applied

 

 

Figure 8: Application of prestress effects as equivalent loads

 

 

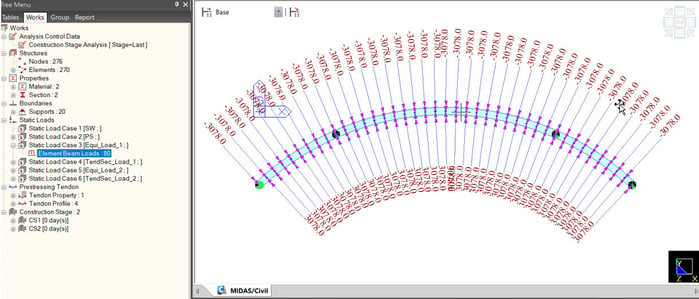
Results comparison:

 

For comparison, two curved beams of the same shape are modeled, one with prestressing tendon

and the other with equivalent-prestress-load applied. Below are the reactions obtained for both

beams.

 

 

 

Figure 9: Reactions obtained due to prestress effects applied as external loads

 

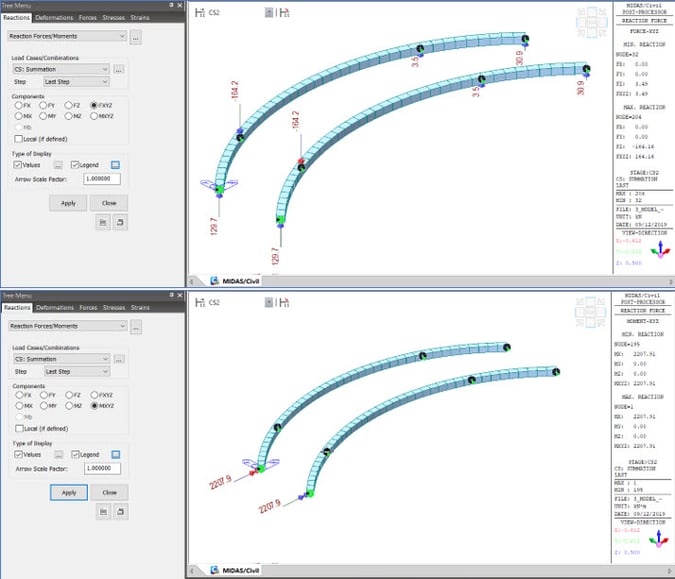
Calculations of Tendon Secondary

 

Now, these reactions can be applied to other curved beams where no intermediate supports are present. Then the effects obtained due to these reactions applied as the external load is tendon secondary effects. The secondary moments in both beams would match.

 

 

Figure 10:Moments obtained due to prestress effects applied as external loads

 

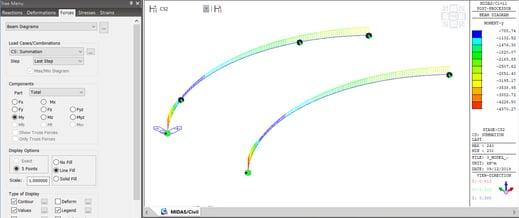
From the above explanations and examples, it is understood that the secondary moment produced by the prestressing needs to be included to compute the ultimate load capacity of continuous prestressed members. The primary effect of the prestressing, which is tendon primary, is to be considered as an internal effect considering the translation of the neutral axis to be applied to the structure, which further could develop the secondary forces due to constraints by the supports.

• ADAPT-Floor (1998), “Software Manual for Analysis and Design of Post-Tensioned Floor Systems,” ADAPT Corporation, 1733 Woodside Rd, Suite 220, Redwood City, Ca 94061, 1998.
• Design of Prestressed Concrete Structures (3rd Edition) - T. Y. Lin & Ned H. Burns - 2
• Lin, T. Y., "Strength of Continuous Prestressed Concrete Beams Under Static and Repeated Loads," ACI Journal, June 1955, Vol. 26, No. 10, pp. 1037-1059.