Get Started midas Civil
Featured blog of this week
📢 To check the entire series, click here
So when the Direct Integration method is used, how should we define the initial load?
In this content, we will discuss the initial load of an analysis using the Nonlinear Direct Integration Method.
A. Definition of initial load for Direct Integration method.
Defining the initial loading conditions is comparatively easier for nonlinear time history analysis using Direct Integration than for the Modal method.
Let's take a look at the same example from Part 1 and see how the initial load is defined for the time history analysis using direct integration.
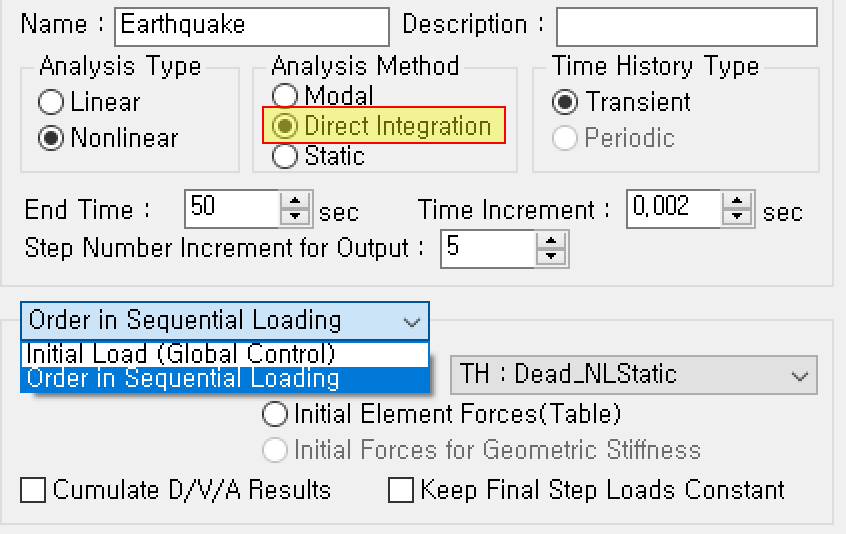
The Analysis Method is selected as Direct Integration, and the End Time, Time Increment, and Step Number Increment for Output are the same as the Modal method in Part 1. (The "Order In Sequential loading" option can be considered for initial load consideration in Part 1, and selecting ST (static load case) is an inappropriate method for this option).
In this content, we will see how to consider the initial load using Initial Load (Global Control) in the Nonlinear - Direct Integration method.
Initial Load (Global Control)
- Active only for Nonlinear - Direct Integration analysis is a method for selecting load cases within Global Control and considering them as initial loads.
- This option allows selecting multiple static Load cases, unlike Time-varying Static Loads where only one load can be selected.
- It is the same as if you used the Time-Varying Static Loads option to perform a Nonlinear - Static analysis on a static load.
%2c%20Static(Analysis%20Method).png?width=908&height=386&name=Figure%202.%20Time%20History%20Load%20Cases%20%20-%20Nonlinear(Analysis%20Type)%2c%20Static(Analysis%20Method).png)
Figure 2. Time History Load Cases - Nonlinear(Analysis Type), Static(Analysis Method)
B. Initial Load (Global Control)
Let's have a look at these options in a little more detail.
1. Time History Global Control
In the Nonlinear-Direct Integration method, the initial load using Global Control is defined as follows.
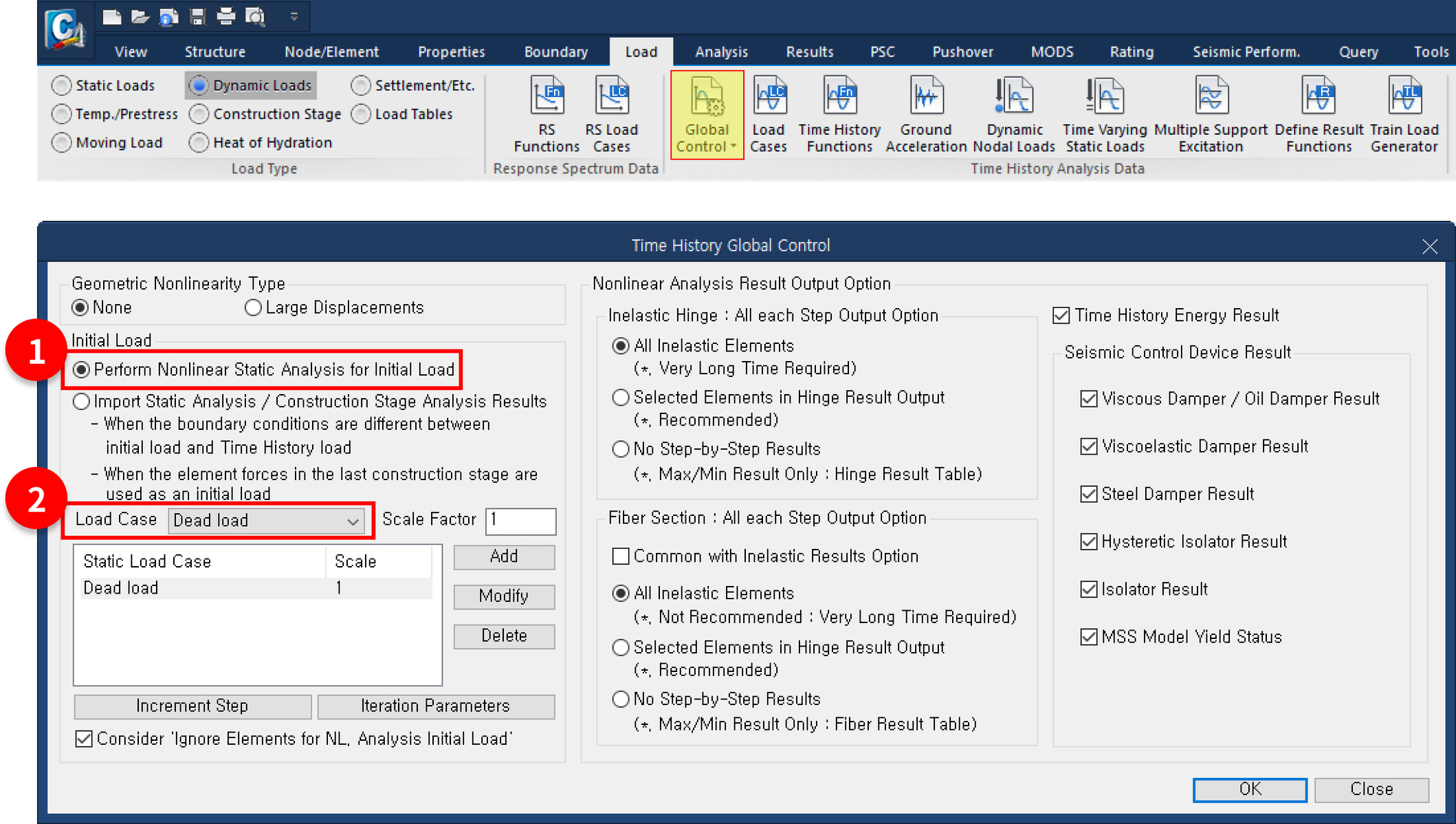
Figure 3. Load > Dynamic Loads > Global Control
-
Select "Perform Nonlinear Static Analysis for Initial Load",
-
Select the static load cases to be considered as initial loads.
With this setting, a nonlinear static analysis of the selected loads is performed. The results are used as initial conditions for the time history analysis.
2. Time History Load Cases
After selecting Initial Load in Time History Global Control, select "Initial Load (Global Control)" in Time History Load Case as follows.
.png?width=908&height=636&name=Figure%204.%20Nonlinear%20-%20Direct%20Integration%20with%20Initial%20Load(Global%20Control).png)
Figure 4. Nonlinear - Direct Integration with Initial Load(Global Control)
The initial load applied in Global Control is considered as the constantly acting initial load. Therefore, "Keep Final Step Loads Constant" is always "Checked On".
"Cumulate D/V/A Results" is an option to select whether to combine the results of the time history analysis with the results of the initial load analysis.
A detailed description of both options is explained in Part 1.
