Get Started midas Civil
Featured blog of this week
Table of Contents
1. Introduction
2. Differential Shrinkage in Steel Composite I
3. Summary
1. Introduction
Reduction in length or volume of concrete which are caused by the change in moisture content or chemical changes is termed shrinkage in concrete.
Now, if we investigate a simple beam that is simply supported, then, it will shrink freely without any restraint. However, if take the example of a fixed beam, then, this shrinking movement will be restrained. Due to this restraint, it will develop stresses. These developed stresses are generally considered secondary stresses.
Now, the question arises, “Why do we observe stresses in steel composite I girder even though it is simply supported?”. The simple answer to this is internal restraint/ internal redistribution. Shrinkage is a concrete phenomenon, and it is not observed in the steel part of the section. Because of different shrinkage strain values across the depth of the section, there will be an internal redistribution of stresses due to composite action.
Shrinkage stress in the concrete can be broken into 3 components in the section: Uniform Axial stress, bending stress, and Eigen Stress as shown in fig 1. If a beam is simply supported, axial and bending stress will be released and eigen stress will remain in the section. Therefore, even though the composite beam is simply supported, I can have shrinkage stresses in the structure. These eigen stresses (locked in stresses) in the case of the simply supported beam are termed shrinkage secondary.
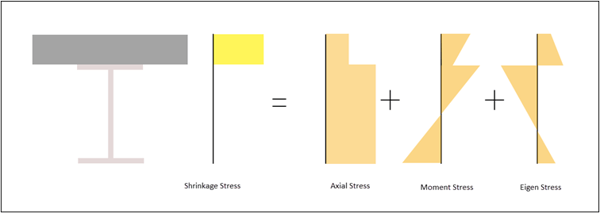
2. Differential Shrinkage in Steel Compoiste I
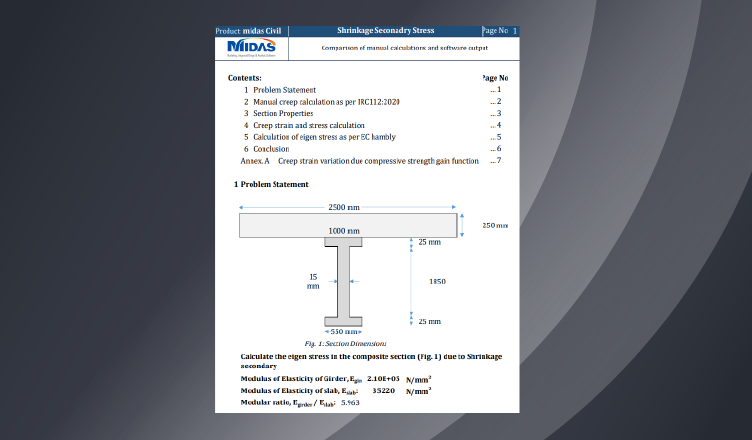
Let us take an example of steel composite I section with the deck as C40/50 material and girder as S355 material. Modular ratio, Es/Ec is 5.9625. The section dimensions are given in Fig 2. with composite section area as 1.600714+005 mm2 and Iyy as 7.77081e+10 mm4. A simply supported beam girder of 30 m was modeled along with the construction stages. In CS1, the girder was activated while in CS2, the deck part of the section was activated with the age of 7 days even though shrinkage begins on the 3rd day. Further, CS3 was given a duration of 10000 days which means the age of the deck at end of CS3 is 10007 days.
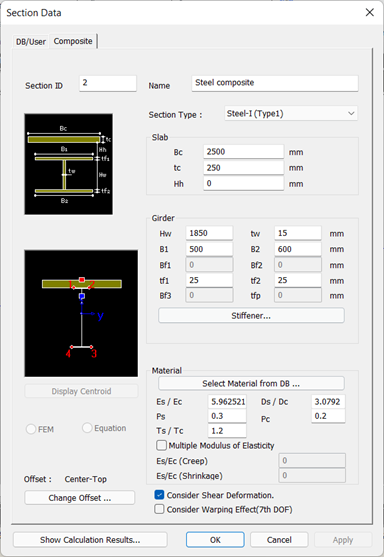Figure 2. Sectional details of Steel Composite sectionShrinkage was calculated as per European code and compressive strength gain function, as well as the creep in the beam, was ignored. Shrinkage primary denotes the shrinkage caused from the activation day to the end observed day. For this case, we will see shrinkage strains from 7 to 10007 days. Shrinkage strain from day 3 to day 7 is 3.83e-5 while shrinkage strain from day 3 to day 10007 is 3.36e-4. Therefore, total shrinkage primary strain will be 3.36e-4 – 3.83e-5 = 2.97e-4. Therefore, the corresponding shrinkage primary stress will be 2.97e-4 * 3.522 e4 = 10.472 MPa as shown in Figure 3.
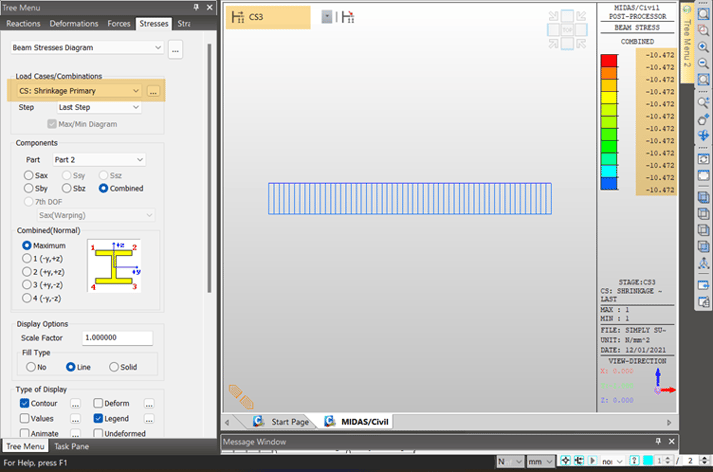Figure 3. Shrinkage primary stress in deck at end of CS3
Now, this stress will be uniformly applied across deck depth. Now, according to fig1., based on the simply supported condition, axial stress and bending stress will get released but eigen stress will remain in the beam. After releasing the axial and bending stress, the stress obtained at different locations based on manual calculations and software are:
|
Location |
Stress (Manual Calculations) (MPa) |
Shrinkage secondary (Midas) (MPa) |
|
Deck Top |
0.832 |
0.832 |
|
Deck Bottom |
2.194 |
2.194 |
|
Steel Top |
-49.357 |
-49.357 |
|
Steel Bottom |
12.365 |
12.365 |
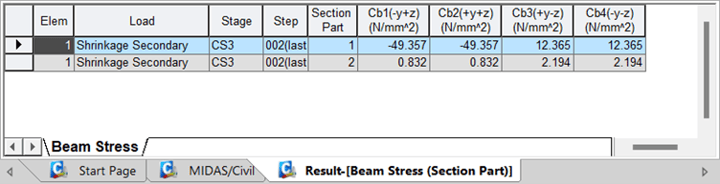Figure 4. Shrinkage secondary stress at end of CS3 in steel and deck parts
*Note: All the calculations have been shown in the document attached below.
3. Summary
Differential shrinkage is crucial to investigate as it can induce additional stresses both in concrete and steel. As verified above in the case of simply supported structure, shrinkage secondary stress results are purely due to eigen stresses which can’t be ignored when designing a section.
.png)
